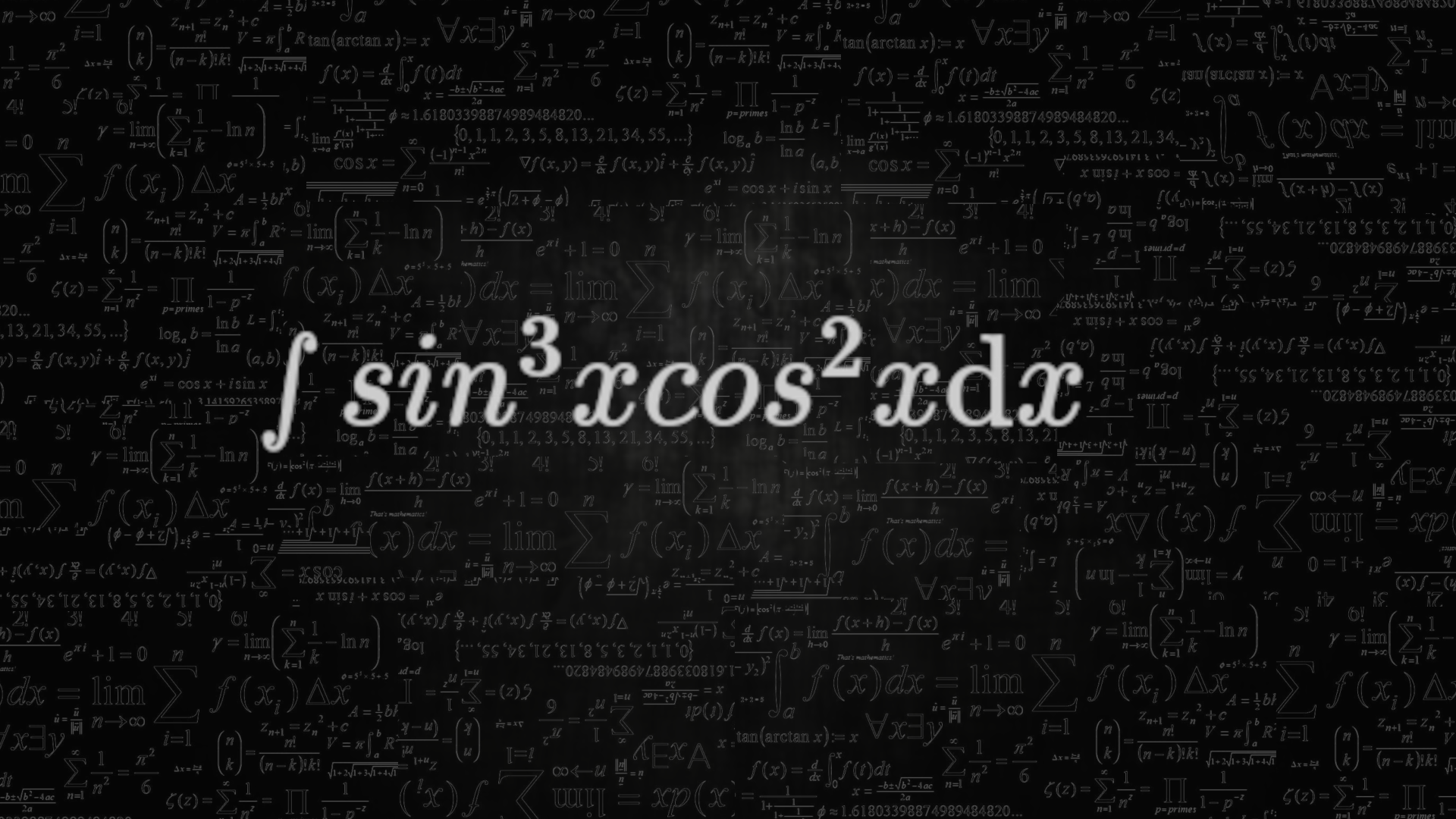How To Integrate sin^3(x)cos^2(x)
Published On :2020-12-06 20:35:00

begin{array}{l} smallint si{n^3}xco{s^2}x{rm{d}}x\\ smallint {bf{si}}{{bf{n}}^{bf{2}}}x{bf{co}}{{bf{s}}^{bf{2}}}x{bf{sin}}x{rm{d}}x\ smallint left( {1 - {{cos }^2}x} right){cos ^2}x;sinx;{rm{d}}x\ By;Substitution;;;;;;\ ;;;;;Suppose Rightarrow z = cosx\ dz = - ;sin xdx\ - smallint left( {{bf{1}} - {z^{bf{2}}}} right){z^{bf{2}}}{rm{d}}z\ smallint {z^{bf{4}}} - {z^{bf{2}}}{rm{d}}z\ Rightarrow frac{{{z^{bf{5}}}}}{{bf{5}}} - frac{{{z^{bf{3}}}}}{{bf{3}}} + c\ Rightarrow frac{{{bf{co}}{{bf{s}}^{bf{5}}}x}}{{bf{5}}} - frac{{{bf{co}}{{bf{s}}^{bf{3}}}x}}{{bf{3}}} + c end{array}