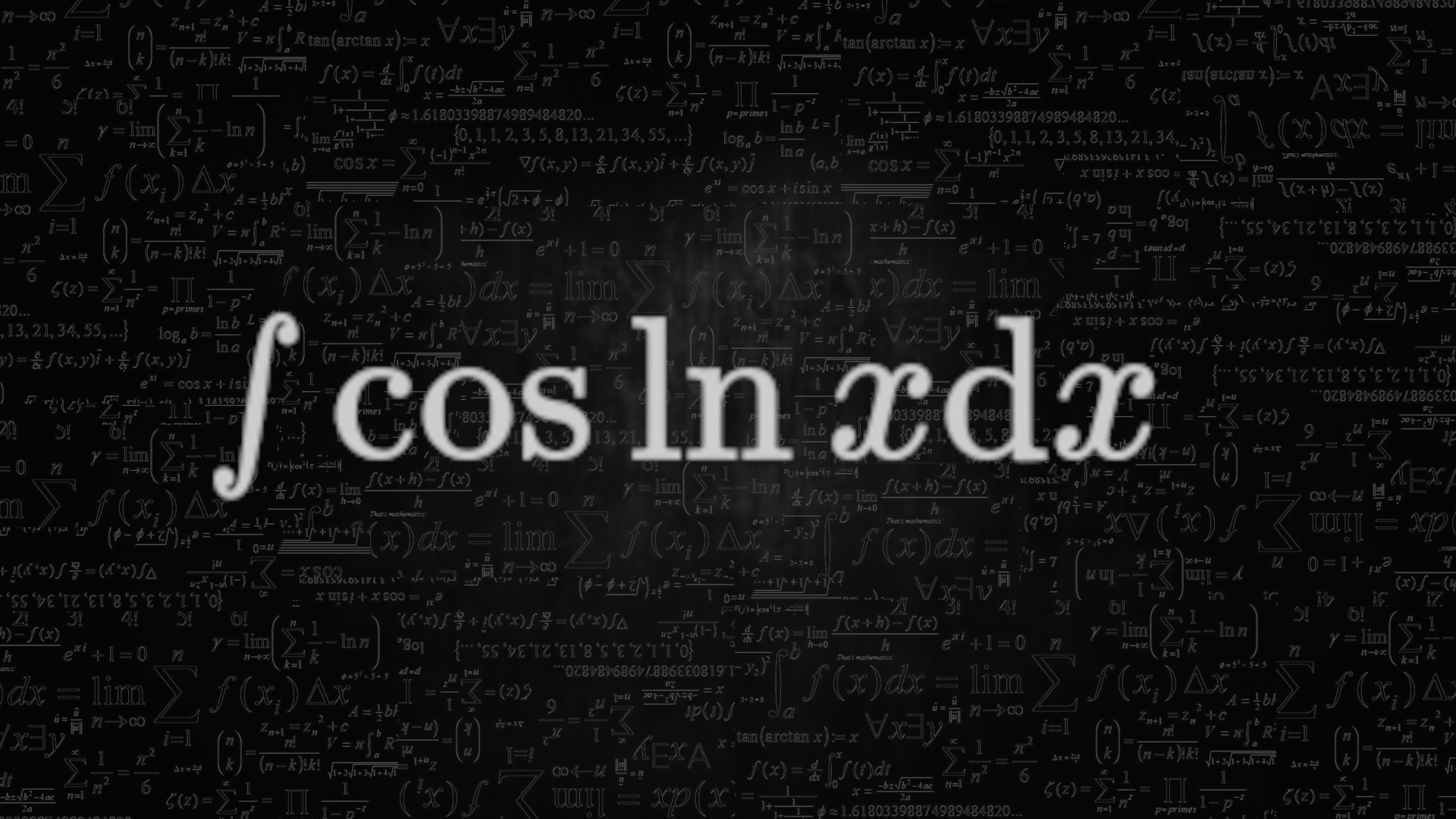How to integrate cos ln(x)
Published On :2021-01-27 17:57:00

[smallint cos ln x{rm{d}}x] begin{array}{l} By;Substitution\ suppose Rightarrow z = ln x\ {e^z} = x\ dz = frac{1}{x};dx\ smallint {{rm{e}}^{rm{z}}}cos z{rm{d}}z\ By;Parts\ Let Rightarrow u = cos z;;;;;;;;;;;;;;;;;;;;;;;;;;;;;dv = {e^z}\ du = - sinz;;;;;;;;;;;;v = {e^z}\ smallint {e^z}cos z;;;dz = {e^z} cdot cos z + smallint {e^z}sin z{rm{d}}z\ By;Parts\ Let Rightarrow g = sin z;;;;;;;;;;;;;;;;;;;;;;;;;;;;;df = {e^z}\ dg = cosz;;;;;;;;;;;;f = {e^z}\ smallint {e^{rm{z}}}cos;z{rm{d}}z = {e^z}cos z + left( {;{e^z}sin ;{rm{z}}; - smallint {e^z}cos z{rm{d}}z;} right)\ 2smallint {{rm{e}}^z}cos z{rm{d}}z = {{rm{e}}^z}sin z + {{rm{e}}^z}cos z\ smallint {{rm{e}}^z}cos z{rm{d}}z = frac{1}{2}left( {{e^z}sin z + {e^z}cos z} right) end{array}